Markov Chain Calculator
Enter the number of states (between 2 and 10):
Enter the transition probabilities for each state:
Enter the initial state probabilities:
Enter the number of steps:
Markov Chain Calculator: Analyze Transition Probabilities Easily
Use our Markov Chain Calculator to compute state probabilities across discrete time steps. Whether you're studying stochastic models or modeling decision systems, this tool simplifies complex Markov chain analysis for you.
Markov chain definition + example calculation, to help you use our Markov Chain Calculator!
A Markov chain is a random process that transitions between states with fixed probabilities, where the next state depends only on the current one (not the past). Common in fields like finance, machine learning, and queueing theory, they help model processes like customer behavior or system reliability.
Markov Chain Visualization
The image below shows how transition probabilities guide the system from one state to another:
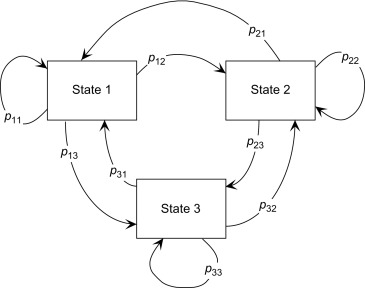
Image credit: ScienceDirect - Markov Chain
Let's see an example calculation, step by step.
In this example we will walk through a simple Markov Chain calculation using a real-world example involving a student’s daily routine.
Scenario
A typical student can be in one of the following three states:
- S: Studying
- L: Sleeping
- C: Socializing
Transition Matrix (P)
S L C
S [0.6, 0.3, 0.1]
L [0.2, 0.7, 0.1]
C [0.3, 0.3, 0.4]
Initial State Vector (π₀)
The student starts the day studying:
π₀ = [1, 0, 0]
Goal
Find the probabilities of the student being in each state after 2 steps (π₂).
Step 1: Multiply π₀ × P
π₁ = [1, 0, 0] × P
= [0.6, 0.3, 0.1]
This is the distribution after one step.
Step 2: Multiply π₁ × P
π₂ = [0.6, 0.3, 0.1] × P
= [
0.6×0.6 + 0.3×0.2 + 0.1×0.3,
0.6×0.3 + 0.3×0.7 + 0.1×0.3,
0.6×0.1 + 0.3×0.1 + 0.1×0.4
]
= [0.45, 0.39, 0.16]
Final Result (π₂)
After 2 transitions, the probability distribution is:
- Studying (S): 45%
- Sleeping (L): 39%
- Socializing (C): 16%
Behind the Scenes: How the Calculator Works
The calculator uses linear algebra to compute the updated state probabilities:
- At each step:
πₙ = π₀ × Pⁿ - This models the evolution of the system over time.
This example can be used in order to simulate the probabilities of numerous situations. Our calculator can help you simulate different situations, so you can have a clear idea of the probabilities after an amount of steps. Try entering this matrix in the calculator to see it in action! The exact reasoning and calculation procedure is used by our Markov Chain Calculator
Key Components in Markov Chains
- The following are the basic components needed in order to simulate a markov chain and calculate the state probabilities:
- Transition Matrix (P): Shows the probability of moving from one state to another.
- Initial State Vector (π₀): Describes the starting likelihood of being in each state.
How to Use the Markov Chain Calculator
- Input your transition matrix – probabilities of moving between states.
- Enter the initial state probabilities – your system’s starting point.
- Choose the number of steps – how many transitions you want to analyze.
- Click "Calculate" – get the probability distribution at your chosen step.
Frequently Asked Questions (FAQ)
What is a Markov chain?
A Markov chain is a type of mathematical model that describes a system which moves between different states, where each move (or transition) is based entirely on the current state — not the previous history. The process is governed by fixed probabilities, and it’s widely used in fields like statistics, economics, computer science, and even biology to predict likely outcomes over time.
How do I create a transition matrix?
To build a transition matrix, start by listing all the states your system can be in. Then, determine the likelihood of moving from each state to every other state in a single time step. These probabilities form the rows of your matrix — and it’s essential that each row adds up to exactly 1 (or 100%) to accurately reflect a valid probability distribution.
What does the initial state vector represent?
The initial state vector shows the starting point of your system. It indicates the probability of being in each possible state at the beginning of the process. For instance, if your vector is [1, 0, 0], that means your system starts entirely in the first state with no chance of starting in any other. If it's [0.4, 0.6, 0], then there’s a 40% chance you're in state 1 and 60% chance in state 2 at the beginning.
Can I use this calculator for large or complex systems?
Yes, absolutely! Our calculator supports up to 10 distinct states, which is sufficient for most educational, academic, or practical use cases. You can define full transition logic for each one, enabling you to model systems ranging from simple to moderately complex with ease.
What do the results actually tell me?
Once you input your data and run the calculation, the output you receive is a vector showing the probability of the system being in each state after the number of steps you chose. It helps you visualize how your system is expected to evolve over time. Whether you're modeling customer behavior, predicting future events, or analyzing decision paths — this distribution gives you deep insight into potential outcomes.
Is this calculator useful for research or classroom learning?
Definitely. This tool is built to be intuitive and helpful for students, educators, data scientists, and professionals alike. Whether you're teaching a lesson on stochastic processes, writing a research paper, or just exploring how systems evolve step by step — the calculator provides accurate, fast, and easy-to-understand results.
🔍 Ready to Try It Out?
Our Markov Chain Calculator helps you visualize and analyze how systems change over time, based purely on probability. Just enter your transition matrix and starting conditions, choose how many steps you want to simulate, and hit "Calculate". In seconds, you’ll see a full breakdown of where your system is likely to be after each transition.
It’s a great way to explore randomness, predict patterns, or support your data-driven projects — whether you're in the classroom, a lab, or the real world.